| September 14, 2022
Название CAP-теорема (читается “кап теорема”), а точнее сам акроним получен от первых букв трёх свойств, которые теорема, собственно, и рассматривает:
- Consistency - непротиворечивость или согласованность
- Availability - доступность
- Partition tolerance - устойчивость к секционированию
Теорема гласит, что распределённая система может обеспечивать не больше двух из трёх упомянутых свойств, и, она активно используется в проектировании распределённых систем. Давайте подробнее рассмотрим каждое из этих свойств.
Теория
Свойства теоремы CAP
Если речь идёт о распределённых системах, то в воздухе где-то рядом витает пресловутый термин - “микросервисы”. Расскажу о свойствах CAP-теоремы на примере микросервисной архитектуры.
Consistency
Согласованность означает, что все клиенты одновременно видят одни и те же данные, к какому бы узлу они ни подключились.
Что это означает? Что в любой момент времени, на всех узлах, после изменения, данные будут согласованными, то есть - одинаковыми и наиболее актуальными. Рассмотрим следующий пример, как это могло бы выглядеть в реальной архитектуре:
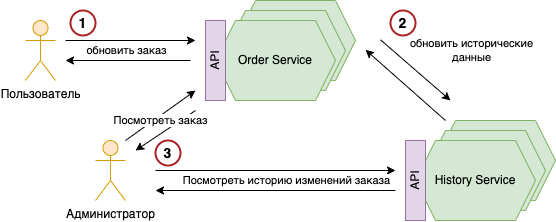
- Пользователь обновляет собственный заказ в созданном специально для этого сервисе.
- Ещё до того, как Пользователь получит ответ от Order Service, распределённая система заботится о согласованности данных и сохраняет детали внесённых пользователем изменений в специализированный сервис - History Service.
- После изменения, внесённого Пользователем в систему, Администратор получит самые актуальные данные из любого инстанса любого сервиса - будь-то любой инстанс Order Service‘а, который вернёт детали пользовательского заказа, или же History Service, любой инстанс которого, вернёт актуальную историческую информацию о внесённых изменениях.
Availability
Доступность означает, что любой клиент, запрашивающий данные, получает ответ, даже если некоторые из узлов недоступны.
Примером, тут может быть распределённая система, развёрнутая в Kubernetes:
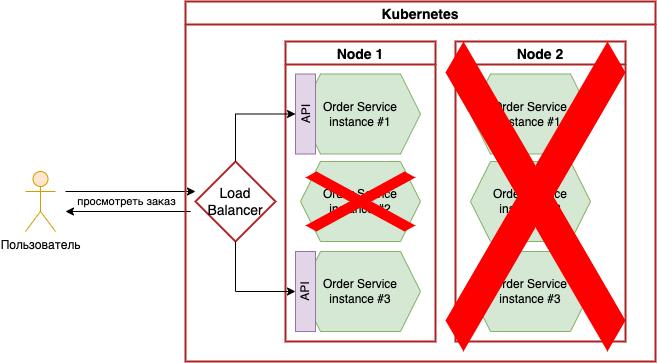
На схеме выше, изображена распределённая система, размещённая в Kubernetes, у которой вышли из строя как целый узел Node 2, так и отдельный инстанс сервиса из узла Node 1. При этом, система продолжает реагировать на запросы пользователя и возвращает данные, не обязательно согласованные.
⚠️ В этом примере, Kubernetes я использовал для удобства изображения и более прикладного примера. Сам Kubernetes здесь никакого значения для свойств CAP-теоремы не несёт и служит скорее иллюстрацией одного из инфраструктурных решений.
Partition tolerance
Устойчивость к секционированию означает, что система продолжает работать вопреки нарушению связи в сети, между её узлами.
Примером послужит следующая схема:
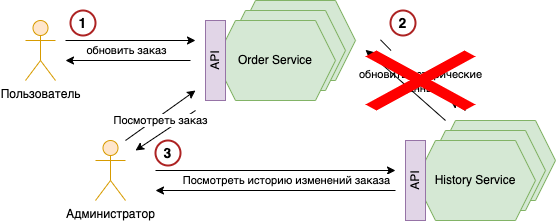
Это та же схема, которая используется для иллюстрации примера с согласованной системой, с одним изменением - на 2ом шаге работы описанного выше алгоритма, связь между Order Service и History Service нарушена.
Свойство Partition tolerance гласит, что в этом случае, распределённая система должна продолжить нормально функционировать.
Классификация распределённых систем
Теперь, когда мы рассмотрели свойства CAP-теоремы и выяснили, что из всех трёх свойств, любая распределённая система может поддерживать только два, самое время поговорить о классификации систем.
Классификация распределённых систем производиться согласно поддерживаемым свойствам CAP-теоремы.
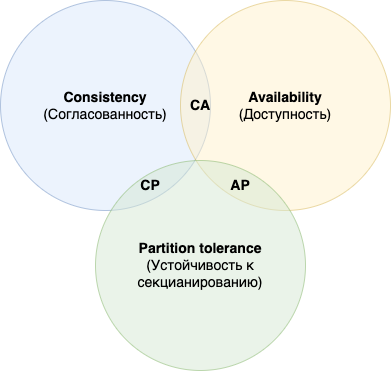
На схеме выше, каждое свойство изображено кругом. Каждый круг пересекает два других круга. На три круга получается три пересечения и они носят название по первым буквам свойств, которые пересекаются. Именно эти двухбуквенные сочетания и принято использовать в качестве классов распределённых систем.
Рассмотрим их подробнее:
- CA системы - это согласованные и доступные системы. Такие системы жертвуют устойчивостью к секционированию. Поскольку сетевые сбои неизбежны - такой класс систем не существует в реальных условиях.
- AP системы - это доступные и устойчивые к секционированию системы. Такие системы жертвуют согласованностью.
- CP системы - это согласованные и устойчивые к секционированию системы. Такие системы жертвуют доступностью.
Заключительная часть
Если Вы работаете над созданием собственных микросервисов, или же отвечаете целиком за архитектуру распределённой сети, CAP теорема послужит отличной “пищей для ума” при разработке дизайна и требований новых сервисов.
Список материалов
- [1] 🇬🇧 Доказательство CAP-теоремы - шикарнейший, вообщем-то материал, в котором на пальцах поясняются прицнипы CAP-теоремы, а так же, приводятся её доказательства.
- [2] 🇷🇺 Теорема CAP на Википедии
- [3] 🇷🇺 Книга “System Design. Подготовка к сложному интервью”. В этой книге неплохо и, самое главное, доступно описана CAP теорема.



